Aula Virtual - Prof. Ing. Juan José Grassi
Categorías
Salta cursos disponibles
Cursos disponibles
MATEMATICAS I
Conceptos que incluimos de Matemáticas: Tipos de Números, Unidades de Medición. Sistema decimal y sexagesimal. Funciones. Definición. Diagramas de Venn. Funciones Inyectivas, Sobreyectivas y Biyectivas. Grado de las funciones. Función de 1° grado. Resolución. Representación gráfica de una Función. Sistemas de coordenadas Cartesianas Ortogonales. Polinomios, definición. Operaciones básicas con Polinomios: Suma, Resta, Producto y Cociente. Polinomios de diferentes grados y con una o más variables. Funciones polinómicas. Regla de Ruffini. Teorema del Resto. Raíces de una Función. Aplicaciones Económicas de los Polinomios. Función Cuadrática, definición. Parábola, definición y gráfico. Forma Polinómica, Factorizada y Canónica de una Función. Circunferencia, Elipse e Hipérbola. Funciones Logarítmicas y Exponenciales. Aplicaciones Financieras. Límites. Definición. Funciones por partes. Resolución de límites. Indeterminaciones. Derivadas, definición. Resolución. Aplicaciones Económicas y Financieras. Derivación de Funciones simples. Reglas de derivación. Uso de las tablas de derivadas. Cálculo de pendientes. Derivadas de funciones acotadas.
Profe Grassi
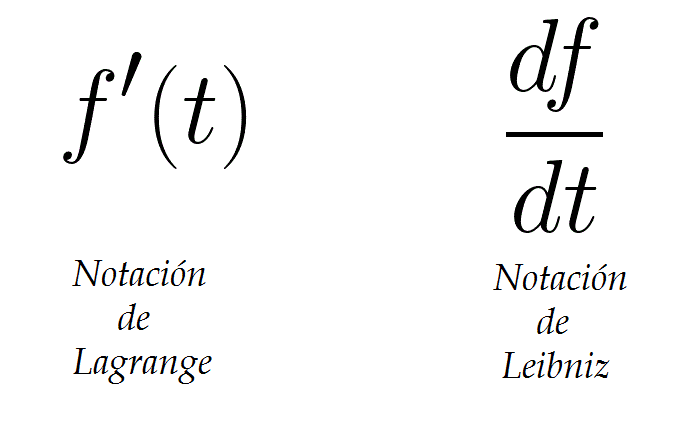
Contenidos de MATEMÁTICAS II:
Repaso de Números, Cálculos y uso de aplicaciones de Cálculo. Funciones Matemáticas: Funciones Inversas, Polinómicas, Exponenciales, Logarítmicas, Trigonométricas. Funciones Particionadas, Funciones Financieras y Económicas. Resolución de Sistema de Ecuaciones. Regla de Cramer. Límites de Funciones. Cálculo diferencial. Indeterminaciones. Regla de L´HOPITAL. Resolución de Funciones Exponenciales y Logarítmicas. Propiedades. Funciones de varias Variables. Derivadas de Funciones de una y más variables. Derivadas por Variables Implícitas. Métodos de Derivación. Cálculo de Máximos, Mínimos y Puntos Críticos de una Función. Ley Oferta y Demanda. Cálculo de áreas encerradas entre Funciones. Integrales definidas e Indefinidas. Integrales Propias e Impropias. Sistemas de Integración por Sustitución y por Partes. Calculo de áreas entre diferentes funciones. Series matemáticas y sus aplicaciones. Polinomios de Taylor y de Mc Laurin
Profe Grassi
PROYECTO INDUSTRIAL - 2025
Físico Química
Expectativas de logro
A partir de los contenidos de este año y en consonancia con el enfoque presentado, se espera que, a partir de la tarea desarrollada, los alumnos:
• Establezcan relaciones de pertinencia entre los datos experimentales y los modelos teóricos;
• Utilicen técnicas y estrategias convenientes para la resolución de problemas de ciencia escolar;
• Describan los procesos fisicoquímicos mediante las expresiones adecuadas, sean éstas simbólicas, matemáticas o discursivas;
• Diseñen y realicen trabajos experimentales de ciencia escolar utilizando instrumentos y/o dispositivos adecuados, que permitan contrastar las hipótesis formuladas sobre las problemáticas vinculadas a los contenidos específicos;
• Interpreten las transformaciones de la materia a partir de una concepción corpuscular y eléctrica de la misma;
• Empleen el lenguaje simbólico y matemático para expresar relaciones específicas entre variables que afecten a un sistema físico;
• Interpreten adecuadamente las ecuaciones químicas y nucleares, como representaciones de procesos, en los que se establecen relaciones de conservación;
• Efectúen predicciones cualitativas y cuantitativas de la evolución de un sistema a partir de las ecuaciones o leyes que describen su evolución;
• Valoren críticamente el impacto de las aplicaciones tecnológicas de distintos procesos físicos y químicos.
Profe Grassi
Matemáticas Superior
PROGRAMA 2025
Álgebra y Geometría:
Unidad N°1: Números de la Matemáticas, funciones, relaciones, gráficos. Concepto de vector. Operaciones con vectores en el plano.
Ecuación de la recta: explícita y vectorial paramétrica. Función lineal.
Unidad N°2: Fractales. Concepto de fractal. Autosimilaridad. Autosemejanza.
Números y operaciones:
Unidad N°3: Números complejos. Ampliación del campo numérico. Distintas formas de representación: polar, binomial y trigonométrica. Operaciones.
Unidad N°4: SERIES. Definición de sucesión. Reglas de formación. Definición de serie. Paso al límite.
Álgebra y cálculo Infinitesimal:
Unidad N°5: FUNCIONES TRIGONOMÉTRICAS. Sistemas de medición. Circunferencia unitaria. Función trigonométrica: dominio, imagen, periodicidad y amplitud.
Unidad N°6: LÍMITE DE FUNCIONES. Concepto de límite. Indeterminaciones. Límite en el infinito.
Límite en un punto. Continuidad de una función en un punto.
Unidad N°7: DERIVADA. Concepto de derivada. Razón de cambio promedio. Derivada en un punto.
Reglas de derivación. Función derivada. Interpretación geométrica de la derivada.
Unidad N°8: ESTUDIO COMPLETO DE FUNCIONES SENCILLAS. Dominio e imagen. Crecimiento y decrecimiento. Ceros. Asíntotas. Máximos y mínimos. Puntos de inflexión. Convexidad. Gráfica de funciones.
Unidad N°9: INTEGRAL. Introducción al cálculo integral. Concepto de integral. Reglas de integración.
Teorema Fundamental del Cálculo. Interpretación geométrica de la integral definida.
Probabilidad y estadística:
Unidad N°10: Experimento, sucesos, datos, estructuración de los datos, Datos Estructurados y desplegados. Espacio muestral. Variable aleatoria. Función de probabilidad. Definición y cálculos de Media, Moda, Mediana y sesgo estadístico. Árbol de probabilidades, Teorema de Bayes. Funciones de distribución discretas:
- Función de Distribución Binomial
- Función de Distribución Geométrica
- Función de Distribución de Poisson
Unidad N°11: Funciones de Distribución de Probabilidades (PDF) Continuas:
- Función de Distribución Uniforme, definición, ejercicios.
- Función de Distribución Bernoulli
- Función de Distribución Normal, definición, condiciones, Parámetros y Estadísticos.
- Función de Distribución Normal Estandarizada (Z). Uso de las tablas, ejercicios.
Profe Grassi
CIRCUITOS ELÉCTRICOS
ESTUDIO E INSTALACIONES
